Autonomous Racing Path Planning
I was recently recruited to lead the path planning team for the new WashU AI Racing Team that will compete in the Formula Student AI competition. Our team is building an autonomous system to drive a pre-built formula-style race car, capable of reaching over 80 mph, around the Silverstone Circuit in England.
The team has just begun, so I am building a path planning module from the ground up. Path planning is designing the optimal race line to complete the course as quickly as possible, based on the perceived information about the race track.
- Technologies and Skills: ROS2, C++, Python, Computational Geometry (
scipy), Convex Optimization (cvxpy) - Fall 2025 to Present
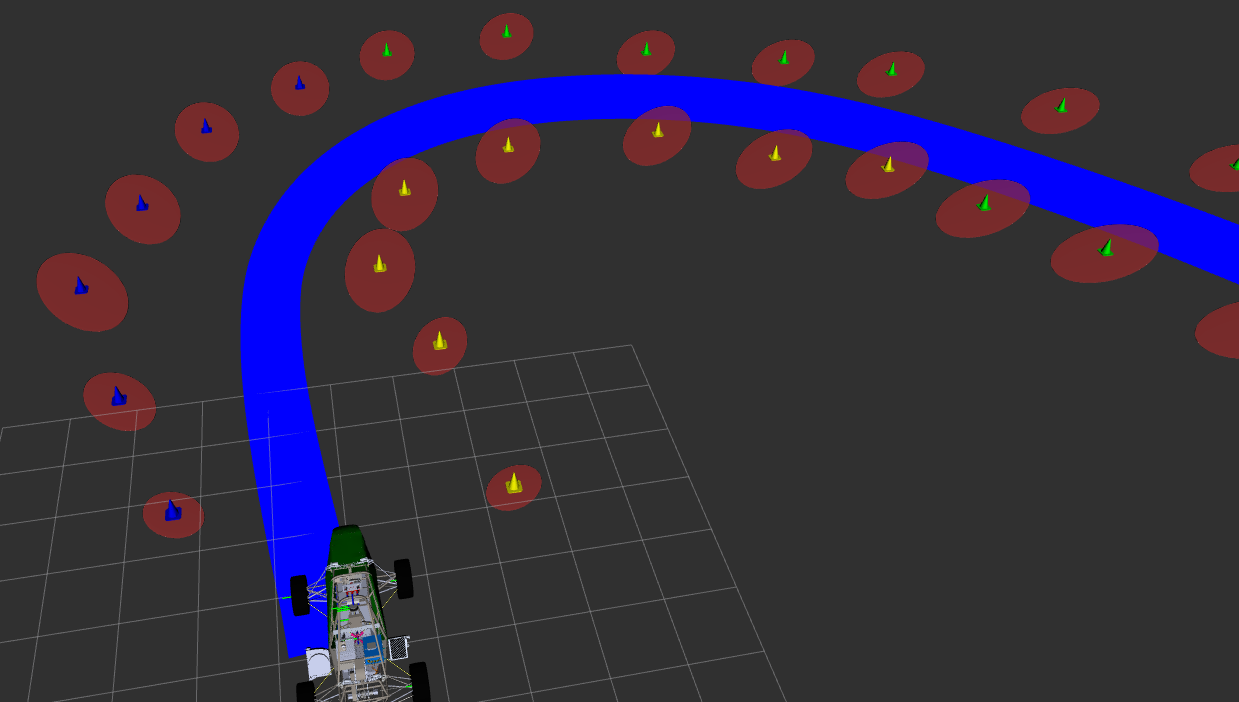
Figure 1: A segment of a minimum-curvature optimized path in simulation.
Approach
The simplest approach to path planning is to follow the middle of the race track. The race track has cones on either side of it, which the state estimation team is tracking. I take the Delaunay triangulation of the locations of the cones, producing a graph where cones are nodes and links between nearby cones are edges. After filtering the edges to only include those that are crossing the race track, the middle of the remaining edges gives us an estimate of the center of the track. Finally, I fit a cubic spline to this to give a rough estimate of the path to follow.
Simple spline fitting works for the first lap before we know the complete layout of the track. However, this approach does not take into account the actual dynamics of the vehicle: it is a lot easier to go fast when you don’t have to turn as much! Therefore, we start with a spline fit around the track as a reference line and seek to find what sort of deviations from the reference line we can make to minimize curvature.
As-is, this would be a nonlinear optimization problem that would be computationally prohibitive to solve: an eternity given the time constraints of the competition. However, it can be manipulated into a quadratic programming problem by making several simplifications, such as assuming that the velocity along the optimal line will be comparable to the velocity along the reference line. This allows us to minimize curvature by only considering acceleration along the optimal line. Forming the problem through quadratic programming with the cvxpy library gives a solution in under a second. The resulting minimum curvature line is considerably faster than the naive middle line.